
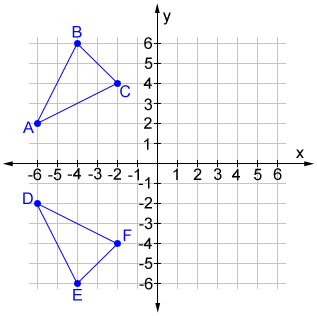
In the present case $m=1/2$ and $q=1/2$, so, just by substituting, Let $\alpha$ be the angle it forms with the $x$-axis and set $u=\cos\alpha+i\sin\alpha$ then you get the symmetric point of $z\in\mathbb For example, if a point ( 3, 7) is present in the first quadrant and we reflect it over the y-axis, then the resulting point will be ( 3, 7). Let's first do it when the symmetry axis passes through the origin. Reflection Over Y-axis When we reflect a figure or polygon over the y-axis, then the y-coordinates of all the vertices of the polygon will remain the same while the sign of the x-coordinates will change. And that's it.I like to use complex numbers for this.

Just remember, any time you take a function and you replace its x with a -x, you reflect the graph around the y axis. Reflections Over the X-Axis and Y-Axis Explained Mashup Math 154K subscribers Subscribe 4. So as predicted, it's a reflection it's a reflection of our parent graph y equals 2 to the x. I have 1 comma one half, I have 0 1, so passes through this point and -1 2. Find the coordinates of the vertices of each figure after the given transformation. Now what about y equals 2 to the -x? Let me choose another colour. 1 one half, 0 1 and 1 2 and I've got my recognizable 2 to the x graph that looks like this. or as a homogeneous matrix y ' 1 1 0 0 tan a 10 0 0 1 y 1 3.10.5 Proof : Reflection in R2 Reflection about the x - axis A point ( x, y ) is reflected. In this activity, students explore reflections over the x-axis and y-axis, with an emphasis on how the coordinates of the pre-image and image are related. And so I'm just going to plot these two functions. But if -x=u then really I just have the 2 to the u values here so these values just get copied over. So -1 becomes 1, 0 stays the same and 1 becomes -1. The triangle is located directly on top of the y-axis, so part of the triangle is on one side of. If I try to graph this function, it does not appear to reflect across the y-axis when it comes time to do the reflection.
#REFLECTION OVER THE Y AXIS HOW TO#
So if I let u equal -x and x=-u and all I have to do is change the sign of these values. This video shows how to reflect a triangle over the y-axis. So those are nice and easy and then to make the transformation, I'm going to make the change of variables -x=u. 2 to the negative 1 is a half, 2 to the 0 is 1, 2 to the 1 is 2. Transformations - Reflect A Triangle Across The Y-Axis mrmaisonet 52. I'm going to change variables to make it easier to transform and I'm going to pick easy values of u like -1 0 and 1 to evaluate 2 to the u. We call the y equals 2 to the x is one of our parent functions and has this shape sort of an upward sweeping curve passes through the point 0 1, and it's got a horizontal asymptote on the x axis y=0. Size does not change, shape may or may not change in orientation. So I want to graph y equals 2 to the x and y equals y equals 2 to the -x together. Mirror image over the x axis or the y axis. Now to see this, let's graph the two of them together. This is a reflection of what parent function? Well it's y equals to the x right? This will be a reflection of y equals to the x. So let's consider an example y=2 to the negative x. So you replace the x with minus x and that will reflect the graph across the y axis. 8.G.1.3 If ABC is rotated 90 clockwise about the origin, what will be the new. Translation 12 units right and 90 rotation about the origin 5. Reflection over the y-axis and translation2 units down C. But how do you reflect it across the y axis? Well instead of flipping the y values, you want to flip the x values. Reflection over the x-axis and translation 2 units down B. All you have to do is put a minus sign in front of the f of x right? Y=-f of x flips the graph across the x axis. Partner A and partner B should share one common point. Each will reflect the given points across the given line of reflection.
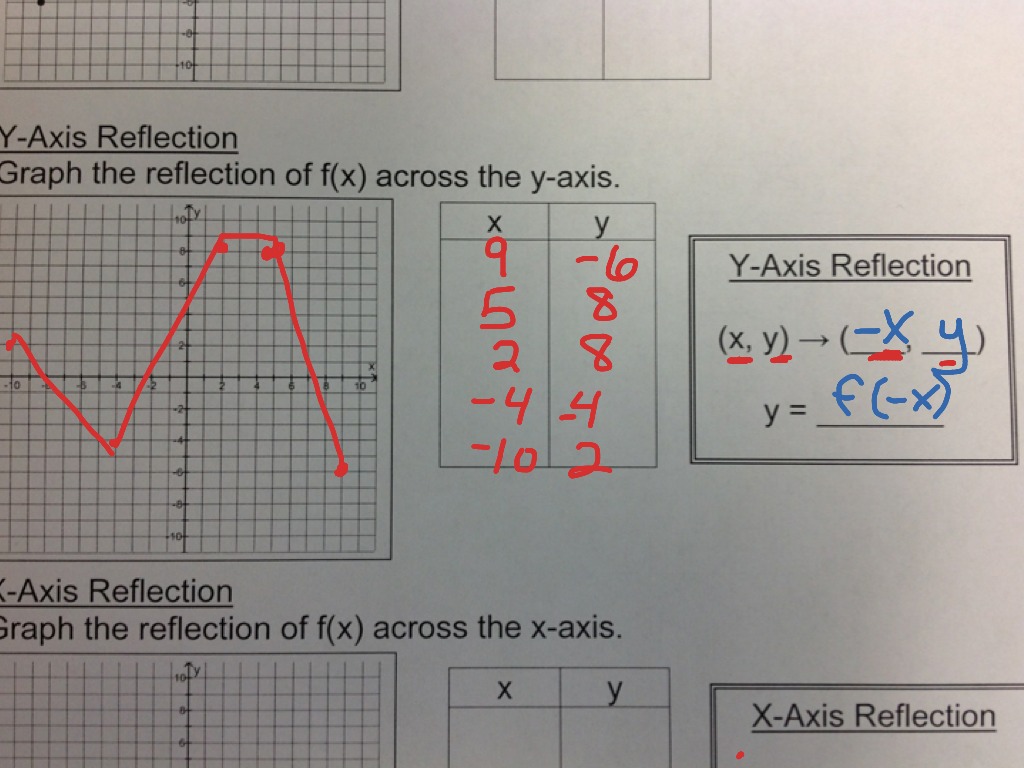
One student will be partner A and the other will be partner B. Now recall how to reflect the graph y=f of x across the x axis. This worksheet covers reflections over the x-axis, y-axis, and over the line yx.


 0 kommentar(er)
0 kommentar(er)
